Find the Number of Subsets of the Set ââ‹math Englishã¢â‹ History Scienceã¢â‹ Art

Euler diagram showing
A is a subset of B,A⊆B, and conversely B is a superset of A.
In mathematics, set A is a subset of a fix B if all elements of A are too elements of B; B is and so a superset of A. It is possible for A and B to be equal; if they are unequal, so A is a proper subset of B. The human relationship of one ready beingness a subset of some other is called inclusion (or sometimes containment). A is a subset of B may also be expressed every bit B includes (or contains) A or A is included (or contained) in B.
The subset relation defines a fractional order on sets. In fact, the subsets of a given gear up form a Boolean algebra under the subset relation, in which the bring together and meet are given by intersection and union, and the subset relation itself is the Boolean inclusion relation.
Definitions [edit]
If A and B are sets and every element of A is as well an element of B, then:
If A is a subset of B, simply A is not equal to B (i.e. there exists at to the lowest degree i element of B which is not an chemical element of A), then:
The empty set, written or is a subset of any set Ten and a proper subset of whatever set except itself, the inclusion relation is a partial club on the set up (the power set of S—the ready of all subsets of S [1]) defined by . We may also partially order by opposite fix inclusion by defining
When quantified, is represented as [2]
Nosotros can prove the statement by applying a proof technique known as the element argument[three]:
Let sets A and B be given. To prove that
- suppose that a is a particular simply arbitrarily chosen chemical element of A
- testify that a is an chemical element of B.
The validity of this technique tin be seen as a result of Universal generalization: the technique shows for an arbitrarily chosen chemical element c. Universal generalisation and then implies which is equivalent to as stated above.
Properties [edit]
- A set up A is a subset of B if and only if their intersection is equal to A.
- Formally:
- A set A is a subset of B if and only if their wedlock is equal to B.
- Formally:
- A finite set A is a subset of B, if and merely if the cardinality of their intersection is equal to the cardinality of A.
- Formally:
⊂ and ⊃ symbols [edit]
Some authors apply the symbols and to point subset and superset respectively; that is, with the same meaning and instead of the symbols, and [4] For case, for these authors, it is truthful of every fix A that
Other authors prefer to use the symbols and to indicate proper (also called strict) subset and proper superset respectively; that is, with the same meaning and instead of the symbols, and [v] This usage makes and analogous to the inequality symbols and For example, if then x may or may not equal y, but if 
Examples of subsets [edit]
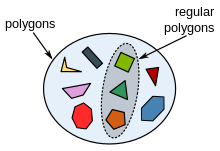
The regular polygons grade a subset of the polygons
- The set A = {ane, two} is a proper subset of B = {one, 2, three}, thus both expressions and are truthful.
- The set D = {1, 2, 3} is a subset (but not a proper subset) of Due east = {1, 2, 3}, thus is true, and is not true (fake).
- Any set is a subset of itself, just not a proper subset. ( is truthful, and is simulated for whatsoever set X.)
- The ready {x: x is a prime number greater than ten} is a proper subset of {ten: x is an odd number greater than 10}
- The set of natural numbers is a proper subset of the set of rational numbers; likewise, the set of points in a line segment is a proper subset of the ready of points in a line. These are 2 examples in which both the subset and the whole set are infinite, and the subset has the same cardinality (the concept that corresponds to size, that is, the number of elements, of a finite ready) as the whole; such cases tin can run counter to one's initial intuition.
- The set of rational numbers is a proper subset of the set of existent numbers. In this example, both sets are infinite, but the latter set has a larger cardinality (or power) than the one-time set.
Some other instance in an Euler diagram:
-
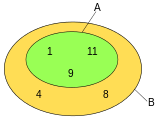
A is a proper subset of B
-
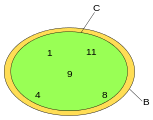
C is a subset only not a proper subset of B
Other properties of inclusion [edit]
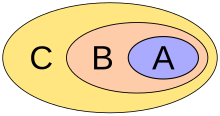
and implies
Inclusion is the canonical partial lodge, in the sense that every partially ordered set is isomorphic to some collection of sets ordered past inclusion. The ordinal numbers are a simple example: if each ordinal north is identified with the gear up of all ordinals less than or equal to n, then if and only if
For the power gear up of a set up Due south, the inclusion partial order is—upward to an order isomorphism—the Cartesian product of (the cardinality of S) copies of the fractional club on for which 
See too [edit]
- Convex subset
- Inclusion order
- Region
- Subset sum trouble
- Subsumptive containment
- Total subset
References [edit]
- ^ Weisstein, Eric W. "Subset". mathworld.wolfram.com . Retrieved 2020-08-23 .
- ^ Rosen, Kenneth H. (2012). Detached Mathematics and Its Applications (7th ed.). New York: McGraw-Loma. p. 119. ISBN978-0-07-338309-v.
- ^ Epp, Susanna South. (2011). Discrete Mathematics with Applications (Fourth ed.). p. 337. ISBN978-0-495-39132-6.
- ^ Rudin, Walter (1987), Existent and complex analysis (3rd ed.), New York: McGraw-Colina, p. half dozen, ISBN978-0-07-054234-1, MR 0924157
- ^ Subsets and Proper Subsets (PDF), archived from the original (PDF) on 2013-01-23, retrieved 2012-09-07
Bibliography [edit]
- Jech, Thomas (2002). Set up Theory. Springer-Verlag. ISBNthree-540-44085-ii.
External links [edit]
-
 Media related to Subsets at Wikimedia Commons
Media related to Subsets at Wikimedia Commons - Weisstein, Eric W. "Subset". MathWorld.
hubbardwhinged1940.blogspot.com
Source: https://en.wikipedia.org/wiki/Subset
































![[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)

![{\displaystyle [a]\subseteq [b].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c0b0cba950301eacc0a11b017b876d2460a33f)








0 Response to "Find the Number of Subsets of the Set ââ‹math Englishã¢â‹ History Scienceã¢â‹ Art"
Post a Comment